|
|
本帖最后由 鬼知道 于 2012-4-22 23:39 编辑
最近忙的跟孙子似的，终于告一段落，开始有点闲功夫了。
身边不少朋友开始创业经商。
反正我对赚钱发达是不抱希望了，就想着挑点实用的，技术性的玩意跟大家分享。反正吃饱了闲着也是闲着，各位就当看着打发个时间吧。
欢迎参与讨论啊，尽量多提问题，有问必答，这样我还能丰富一下，说不定就对谁有用了。
这篇就讲优化(en:Optimizaton, es:Optimizacion)里的线性规划 (en:Linear Programming, es: 不知道...) 吧。实际上只是"管理科学/运筹学" (en:Operatinal Research, es:Investigacion de operaciones)的最最最简单部分。
从一个例子开始：
假设你经营了一个小小的商铺，为了让这个例子尽量简单，你这个倒霉的小商店只能出售两种货品：1)整箱的方便面 2)整箱的软饮料。
作为一个愣头青，你认为顾客们对于方便面和软饮料有着极大的热忱，所有进货都可以售出(迟早)。但是，同样你的采购资金很有限，只有500欧。
一箱饮料进价8欧，一箱方便面进价10欧。而一箱饮料的出售价格是13欧，一箱方便面则是18欧(你还真是个心底善良的商人)。
而方便面批发厂商给了你一些优惠，如果你购买超过10箱方便面，就送你一顶漂亮的帽子(翠绿翠绿的....)。为了这顶帽子，你必须买10箱。 饮料20箱起批，至少买20箱
问题：你该采购多少方便面，多少软饮料? 才能将利润最大化?
这是一个典型的 "线性规划" 问题，上个世纪前半叶，帝国主义亡我之心不死，为了更快，更有效的阻挠世堺人民革命，美国佬开发了这套数学方法用来有效的为空军提供物资补给。后来，有一些吃饱了撑的数学家，经济学家们，发现这种方法可以用来骗国家拨款，就一拥而上，这门技术得到了极大的发展。
回到例子上，理解这样的问题先说得明白几个重要的"江湖用词": 常量, 变量, 目标 和 限制:
常量，最简单，就是不受你意志而改变的量，比如你已共有 500欧，饮料的进价8欧，售价13欧(你也可以更改售价，但那是另一个问题了) 之类的。
变量是你需要在这里作出决定的量，受你意志左右，这里有两个变量 买y1箱方便面, 和买y2箱饮料
目标是你想要"最大化", 比如你的利润 或者 "最小化" 比如货物的占地面积。在这个问题里，你有一个目标 最大化的你的利润。
最大化 用 maximize 来表达，而你的利润公式是 (进价-成本)*数量 。所以这里你有以下目标:
maximize: (18-10)*y1+(13-8)*y2
限制，你可以从字面上理解，就是你苦13的所在，你只有500欧，还有你必须获得的那顶10箱面换来的帽子。
所以:
a) 10*y1+8*y2 <= 500 (采购花销要小于等于500)
b) y1>=10 (面要大于等于 10箱)
c) y2>=20 (饮料至少20箱)
综合起来:
variable(变量): y1, y2
maximize(最大化): (18-10)*y1+(13-8)*y2
constraints(限制): 10*y1+8*y2 <= 500
y1>=10
y2>=20
解法:
1) 手工求解: ............................... 看官，你午饭吃多了吧 .............................
2) 自动求解:
求解这个问题可以用 Excel 自带的 Solver 软件，非常方便简单，有兴趣请google "solver 教程"即可，下面是一个简单的不能再简单的过程，我实在懒得截图，抛砖引玉，抛砖引玉昂。
首先输入，各种玩意：
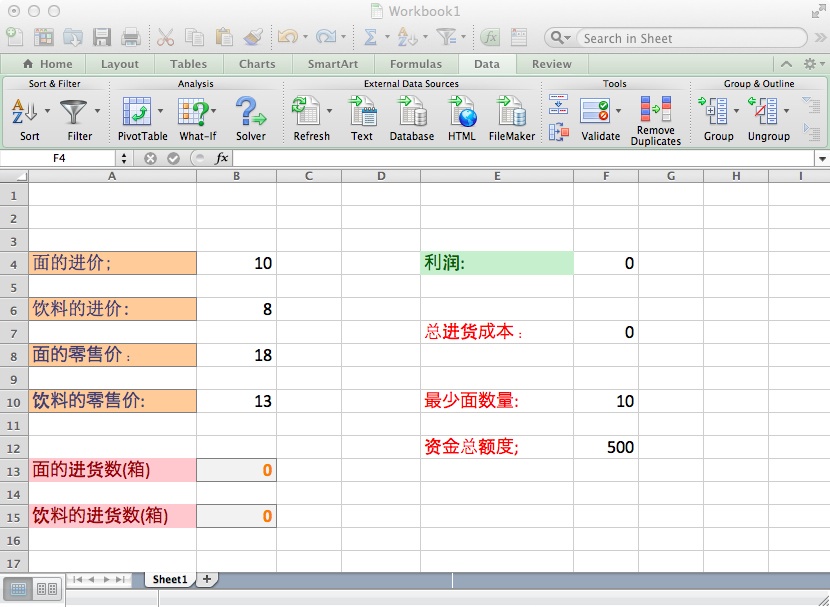
注意，F4单元格，就是"利润"，是一个公式:
F7单元格，进货总成本，也是一个公式：=B4*B13+B6*B15
其他都是常量，就是直接输入的。
然后打开，"Data" (中文版: 数据)选项卡下的 Solver 工具，
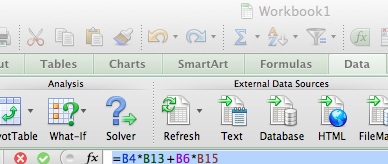
按下面的设置
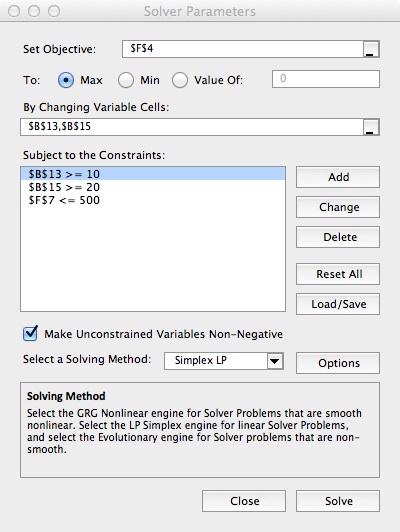
这个窗口设置非常简单，首先是选择目标单元格，就是我们这里的"利润"
然后添加变量单元格，就是你要求解的y1, y2 也就是 面和饮料的采购数量
然后再添加 (Add) 限制单元格，比如F7, 总采购成本 要小于 (<=) 500
然后单击"Solve"，结果如下：
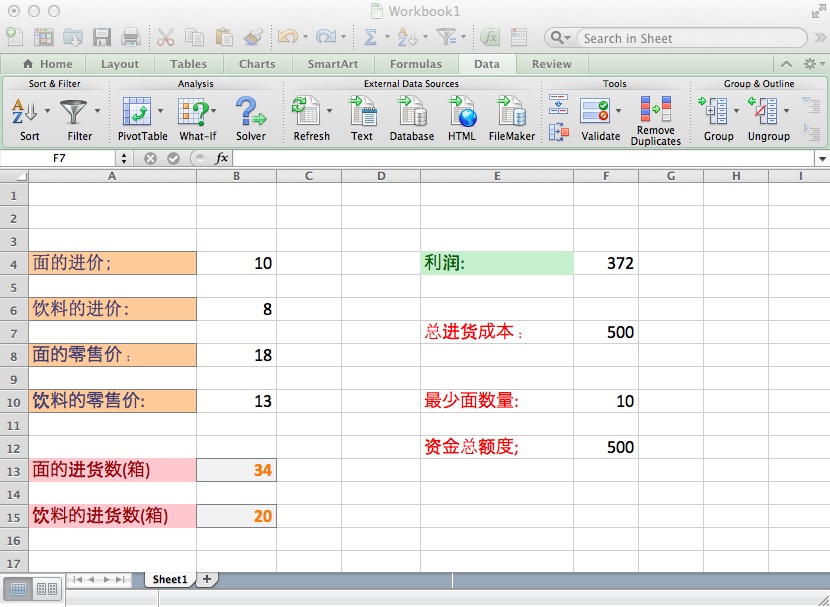
所以你应该买 34箱面，20箱饮料，花费500, 获利372
|
评分
-
查看全部评分
|
[复制链接]
狗仔卡
发表于 2012-4-22 23:25:38
提升卡
喧嚣卡
变色卡
抢沙发
千斤顶
显身卡
楼主
发表于 2012-4-22 23:30:20
该贴发自手机用户
发表于 2012-4-22 23:41:16
发表于 2012-4-23 00:15:25
